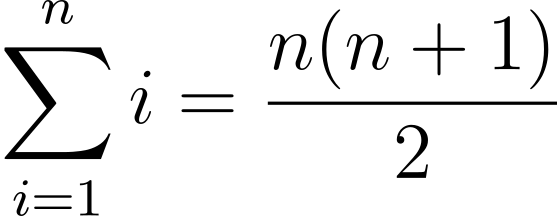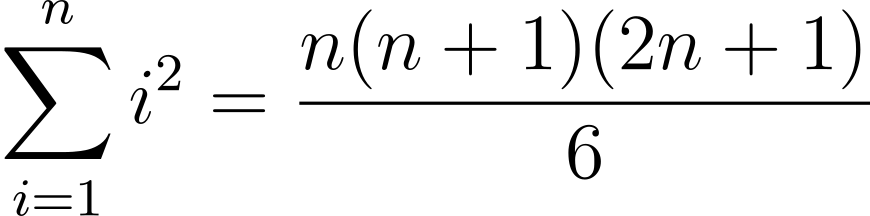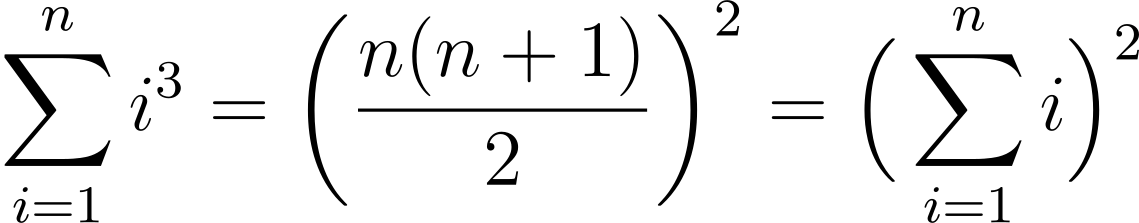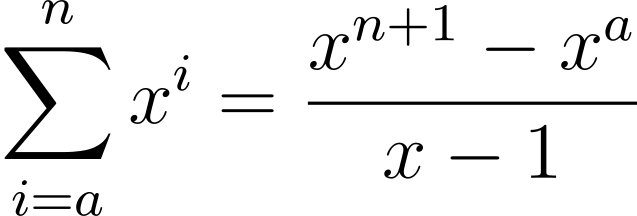An arithmetic progression is a sequence of numbers such that the difference between any two consecutive numbers in the sequence is a constant. So an arithmetic progression with n terms looks like
![]()
a is called the initial term, a + (n – 1)d is called the final term and d is called the common difference.
Let’s investigate what the sum of the terms of an arithmetic progression is. Σ (sigma) is a letter of the greek alphabet that’s used to represent sums. When we write
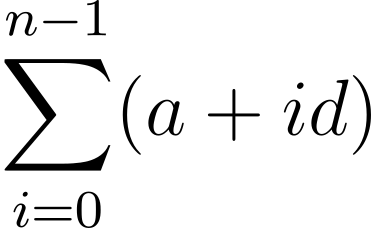
what we mean is we’re looking at a sum of a sequence of numbers of the form a + id. The initial term is formed by substituting i = 0, i.e. a + 0d = a. Subsequent terms are formed by substituting increasing values of i, i.e. a + 1d, a + 2d, … until we reach the final term, which is when we substitute i = n – 1, i.e. a + (n – 1)d. Then we add up all the terms in the sequence.
Here’s a concrete example of an arithmetic progression: 2, 5, 8, 11, 14, 17, 20, 23, 26. Note that ‘opposite’ terms have the same sum: 2 + 26 = 5 + 23 = 8 + 20 and so on. This gives us a nice way to sum the entire arithmetic progression. If we let S = 2 + 5 + 8 + 11 + 14 + 17 + 20 + 23 + 26, then
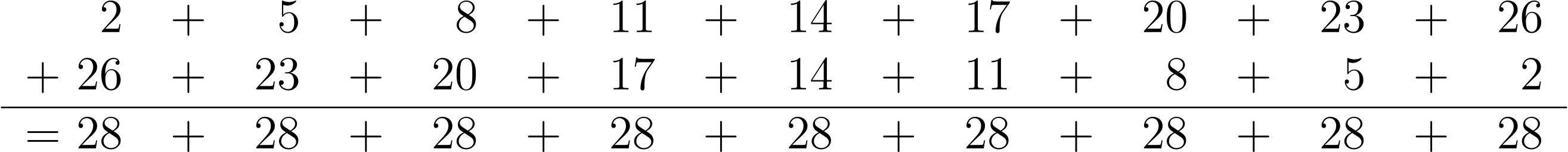
So twice the sum, 2S is equal to the sum of the first and last term (2 + 26 = 28) multiplied by the number of terms (9). Hence S = 28 x 9 / 2 = 126.
Similarly, for a general arithmetic progression, the sum of the first and last term is a + (a + (n – 1) d) = 2a + (n – 1) d. There are n terms in total. Hence the sum is
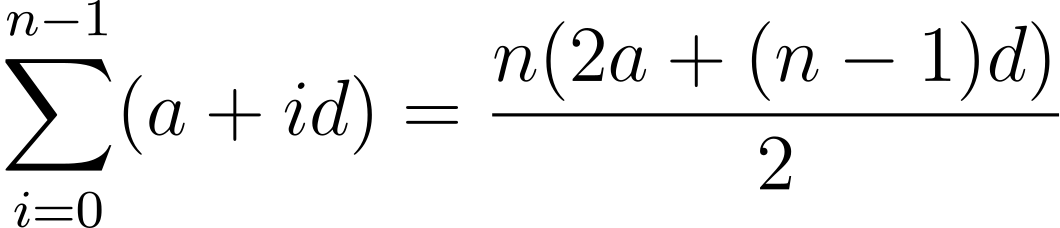
A geometric progression is a sequence such that any two consecutive terms have the same ratio. So a geometric progression with n terms looks like
![]()
Again, let’s investigate the sum
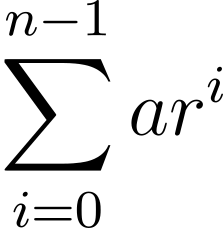
This time, instead of working through a concrete example first, let’s see if you can follow along with the algebra:
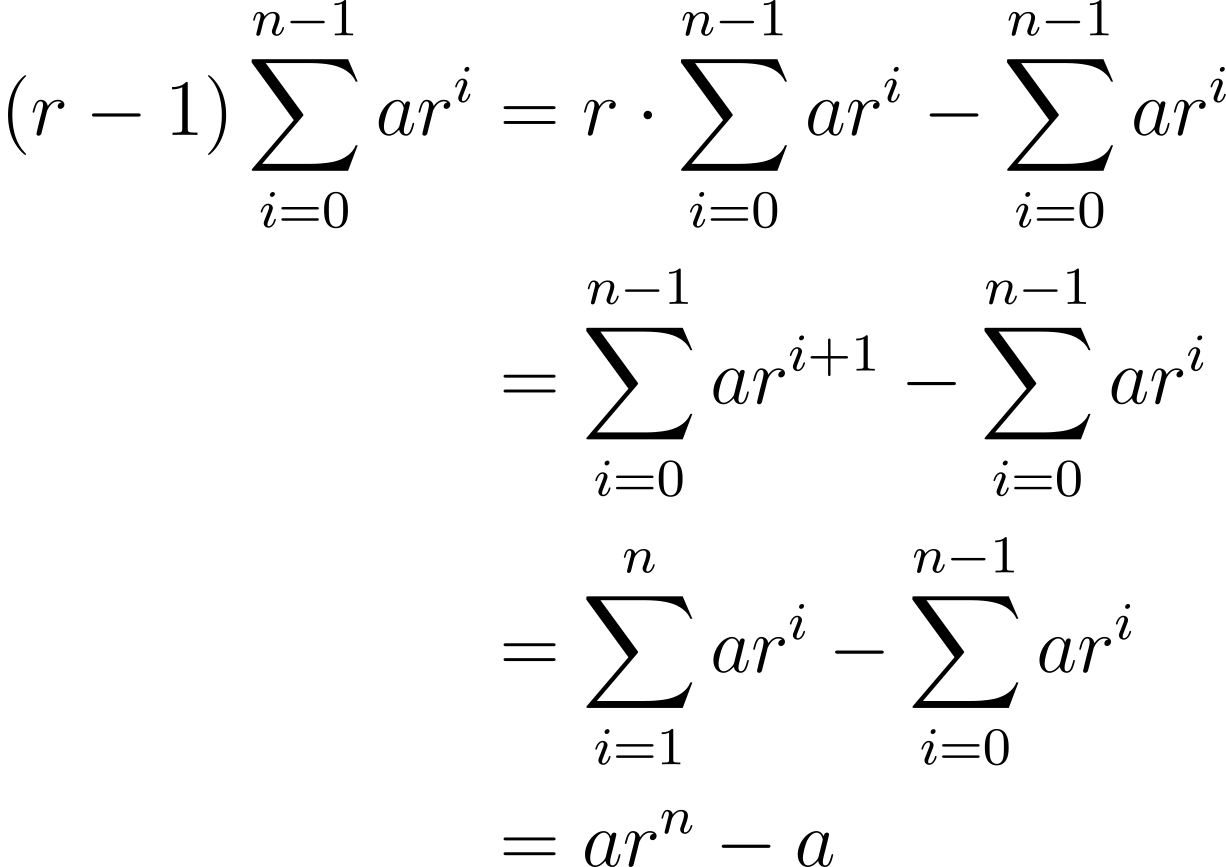
The last equality arises from the common terms in the two sums cancelling out. Hence the sum of our geometric progression is
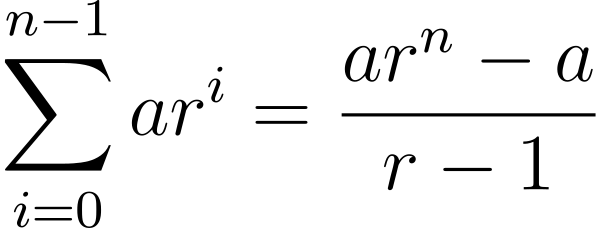
Here are some other sums. Can you prove them?