Polynomials of degree 3 are called cubic polynomials. Cubic equations are of the form
![]()
We can substitute x = y – (b/3a) into the above to transform it into a depressed cubic equation
![]()
where
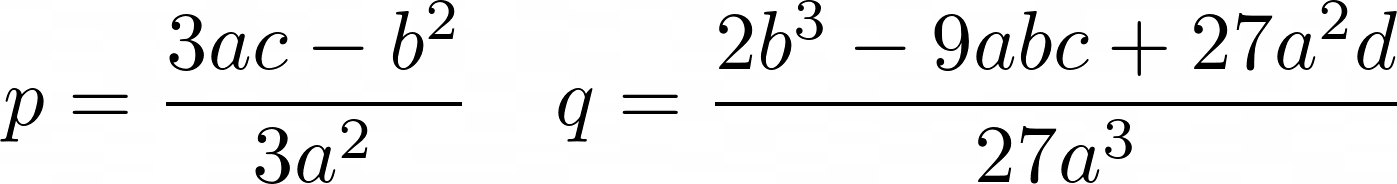
Consider the algebraic identity
![]()
which looks similar to the depressed cubic. Indeed, setting y = a – b, p = 3ab and q = b³ – a³ gives the above depressed cubic. If p = 0, then y³ = –q and so the roots are just the cube roots of –q. If p is non-zero, then b is also non-zero and a = p/3b. Substituting, we have
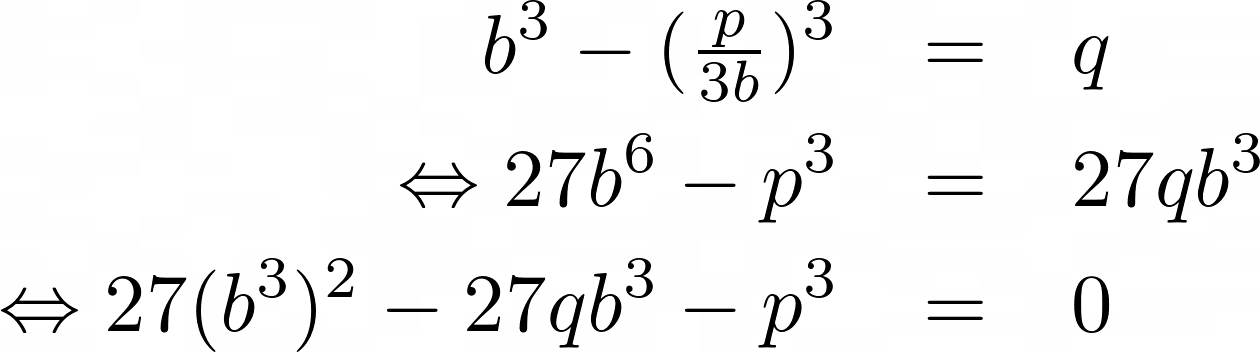
This is a quadratic in b³. Solving, we have
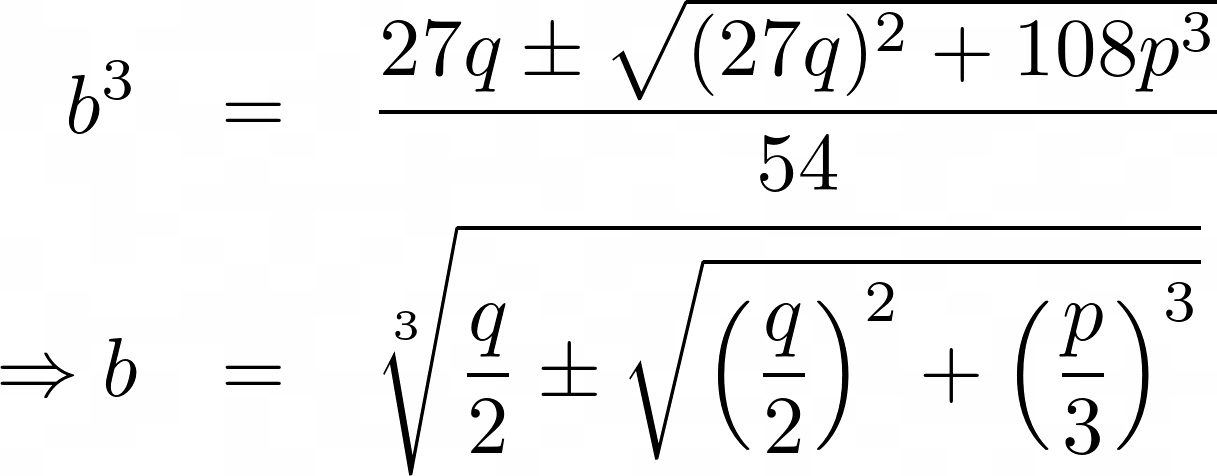
and solving for a gives
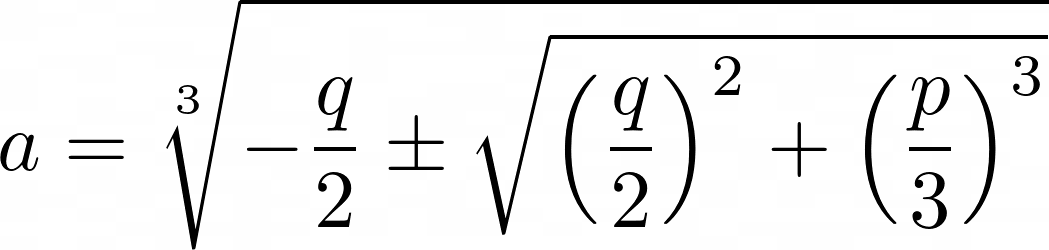
Now we have one root y = b – a of the depressed cubic. Factoring out (y – (b – a)) from it leaves a quadratic which is easily solved.

