A set is a collection of elements.
The cardinality of a set A is the number of elements in A. We write |A| to denote this.
For two sets A and B, if every element of A is also an element of B, we say that A is a subset of B and write A ⊆ B. So |A| ≤ |B|.
The universal set is the set containing all elements being studied. All sets being studied should be subsets of the universal set.
Given a universal set U, the complement Aᶜ of a set A is the set of all elements in U that don’t lie in A. So |A| + |Aᶜ| = |U|.
The union A ∪ B is the set containing all elements that lie in either A or B
The intersection A ∩ B is the set containing all elements that lie in both A and B.
Unions and intersections have commutative, associative and distributive properties.
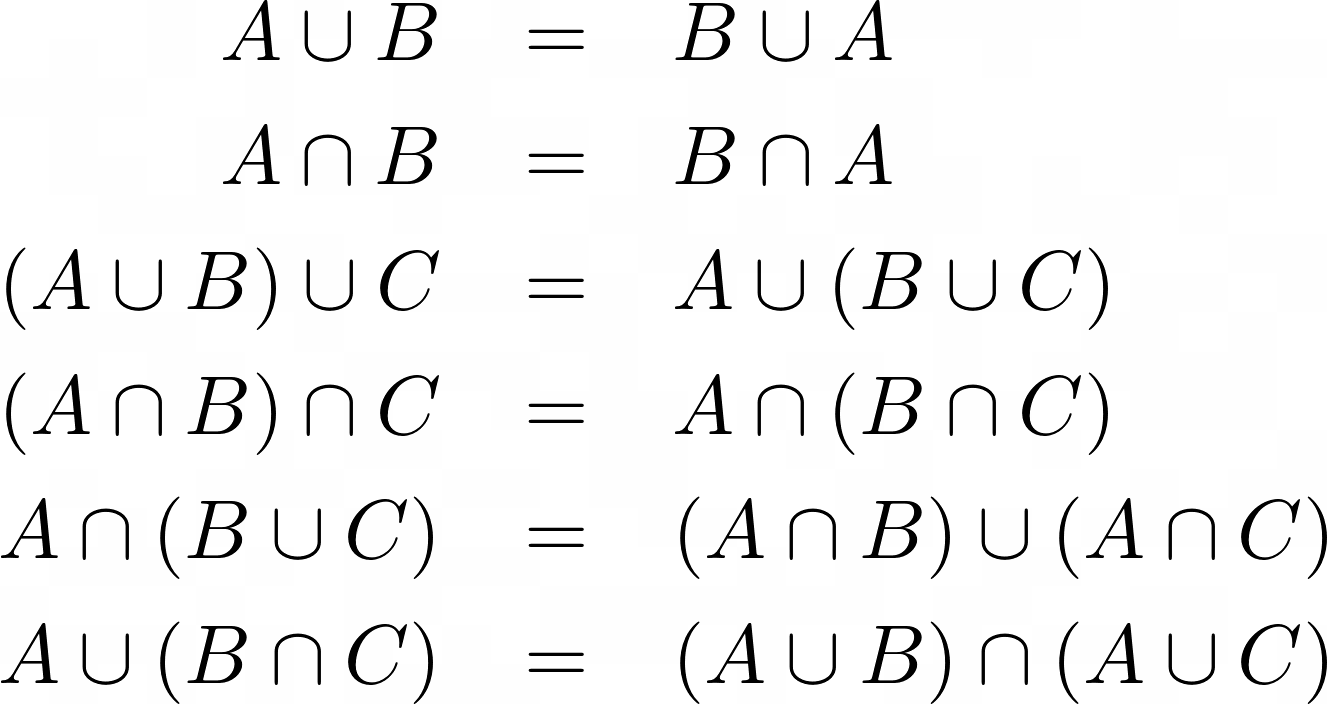
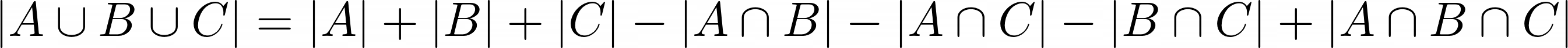
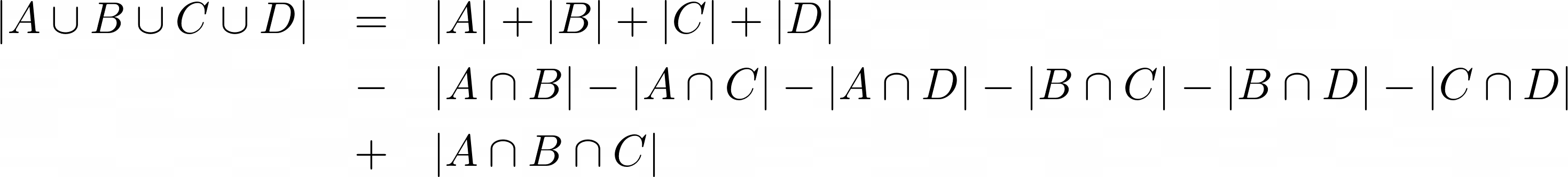
Do you see a pattern? Can you extend this to 5, or even more sets? This is called the Principle of Inclusion – Exclusion (PIE). The general expression is
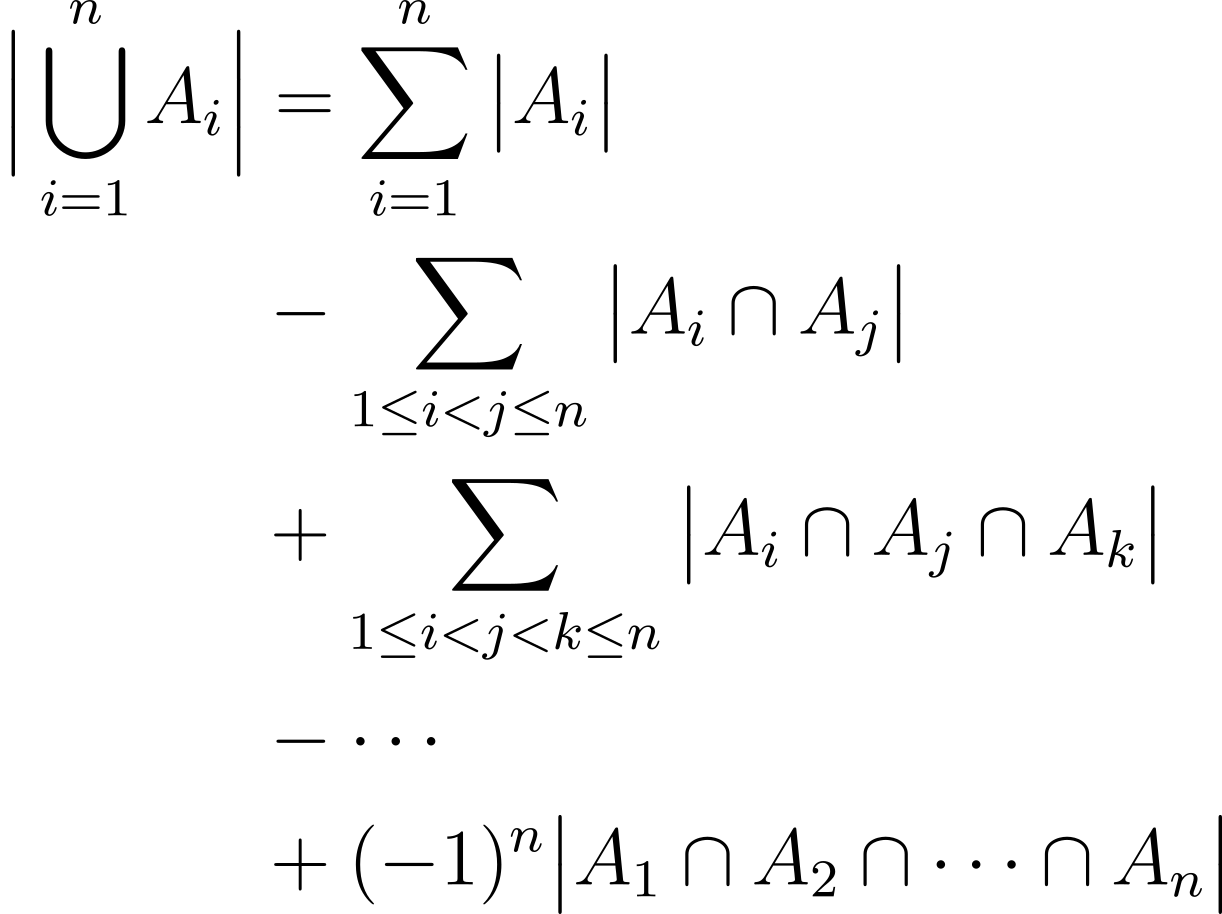
(SMO 2010 Open) Find the number of permutations a₁ a₂ a₃ a₄ a₅ a₆ of the six integers from 1 to 6 such that for all i from 1 to 5, aᵢ₊₁ does not exceed aᵢ by 1.
Let P(i) be the number of permutations such that the digit i + 1 appears immediately after the digit i. By the Principle of Inclusion-Exclusion,
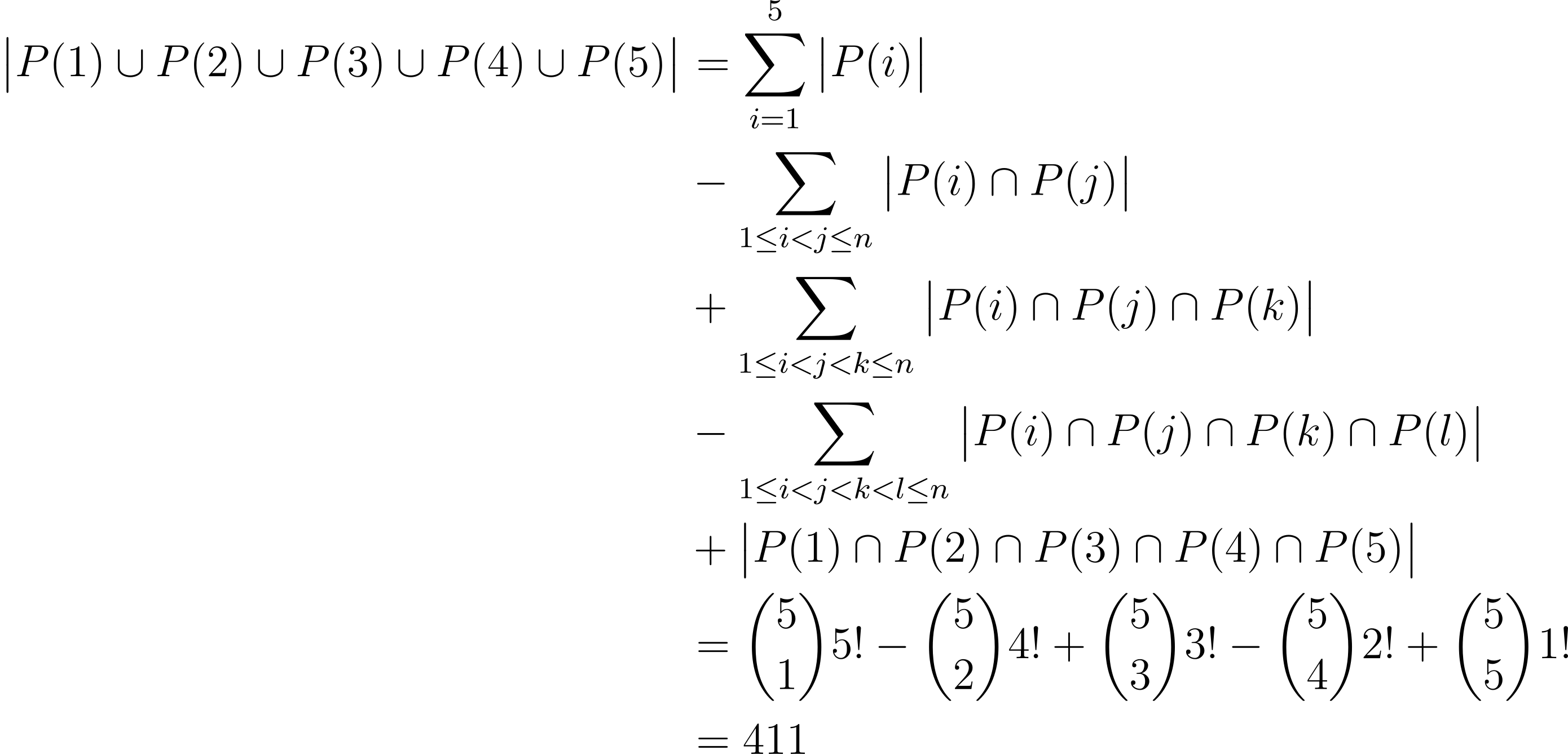
The desired set of permutations is the complement of
within the set of all 6! = 720 permutations of the digits 1 to 6. Hence the desired number of permutations is 720 – 411 = 309.
