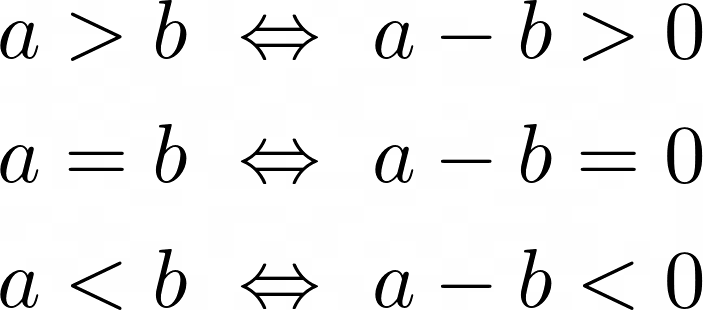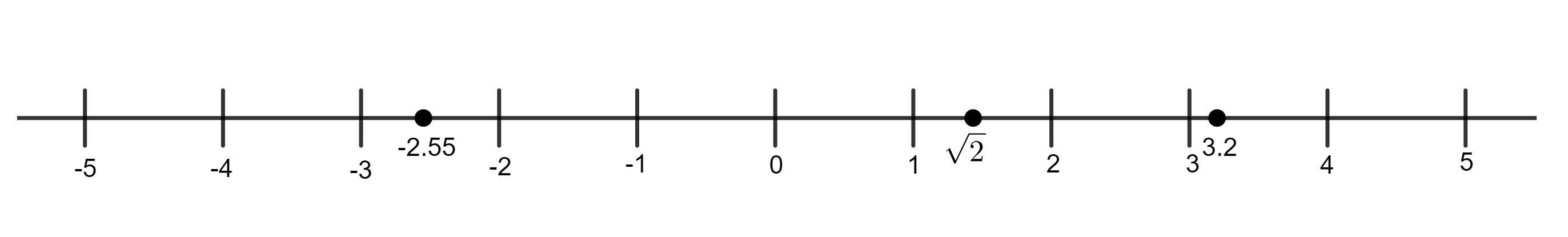
Consider a line extending in both directions towards infinity. Pick a point on it and label it 0. Fix a unit distance and mark off points that are integer multiples of this distance away from 0. The marked points to the right of 0 represent the positive integers, and the marked points to the left of 0 represent the negative integers. Then every point on this line represents a unique real number, and every real number corresponds to a unique point on this line.
Rational numbers Integers and fractional numbers are called rational numbers. Every rational number can be written in the form m/n for some integers m, n (n ≠ 0)
Irrational numbers Numbers whose decimal expansions go on forever and don’t repeat are called irrational numbers.
Every real number is either rational or irrational.
Integer part and fractional part Given a real number a, the integer part of a, denoted by [a], is the largest integer not greater than a. a – [a] is called the fractional part of a, this is denoted by {a}. For example:
[3] = 3, [3.2] = 3, [-3.2] = -4
Thus the integer part of a corresponds to the integer point on the number line to the left of a (or a itself) that is closest to a. The fractional part of a is the distance of a from this point.
Opposite numbers A pair of numbers that differ only in sign are called opposite numbers. i.e. a and –a are a pair of opposite numbers. a is the opposite of –a and vice versa. 0 is the opposite of itself.
Absolute value The absolute value is the distance of the point on the number line from 0. Hence the absolute value of a positive real number is itself. The absolute value of a negative real number is its opposite. The absolute value of 0 is 0. It is always non-negative, and is formed by ignoring any negative sign in front of the number.
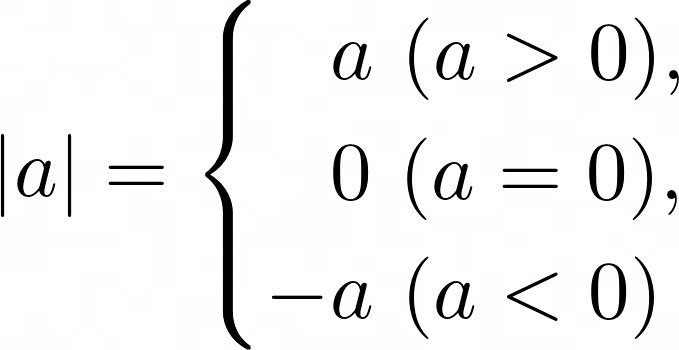
Opposite numbers have the same absolute value.
Reciprocal Given a non-zero real number a, the reciprocal of a is 1/a. 0 does not have a reciprocal.
Comparing real numbers For any two different numbers on the number line, the one on the right will be larger than the one on the left. The positive reals are all larger than 0 and the negative reals are all smaller than 0. Among two positive reals, the one with the larger absolute value is larger. Among two negative reals, the one with the larger absolute value is smaller.
Properties of the real numbers
- For all real numbers a, we have a² ≥ 0, |a| ≥ 0. Equality holds precisely when a = 0.
- If √a is a real number, then a ≥ 0.
- The real numbers are ordered, for any pair of distinct real numbers, one will be greater than the other.
- For any two real numbers a, b, we have