Laws of addition For any real numbers a, b, c, we have
(A) Commutativity a + b = b + a
(B) Associativity (a + b) + c = a + (b + c)
Laws of multiplication For any real numbers a, b, c, we have
(A) Commutativity ab = ba
(B) Associativity (ab)c = a(bc)
(C) Distributivity (a + b)c = ac + bc
Signs For any real numbers a, b,
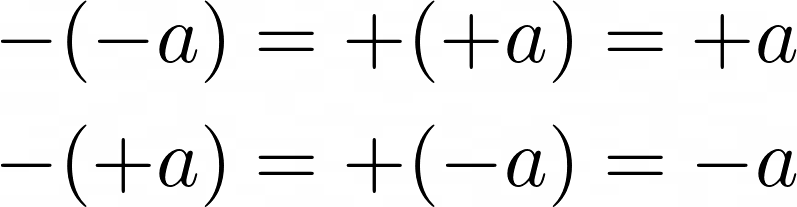
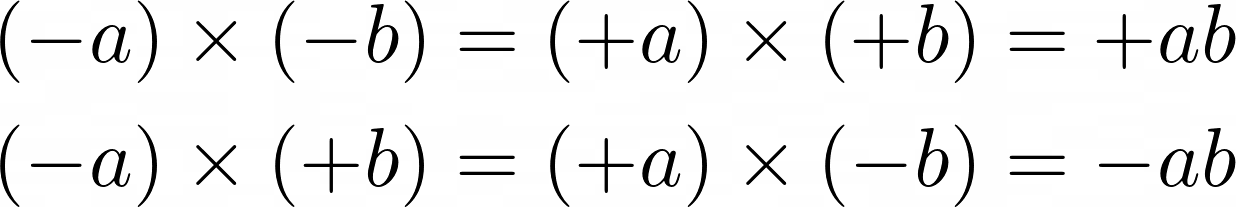
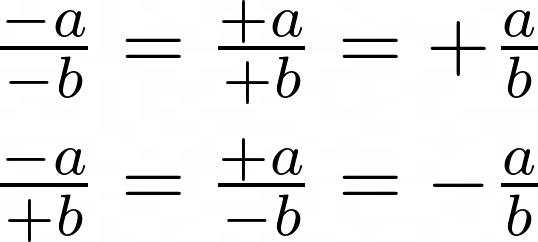
When an even number of negative numbers are multiplied together, the result is a positive number. When an odd number of negative numbers are multiplied together, the result is a negative number.
Exponentiation Multiplying n copies of the number a together is called exponentiation. We write 
. a is called the base, n is called the exponent and aⁿ is called the power.
Laws of exponentiation For positive real numbers a,
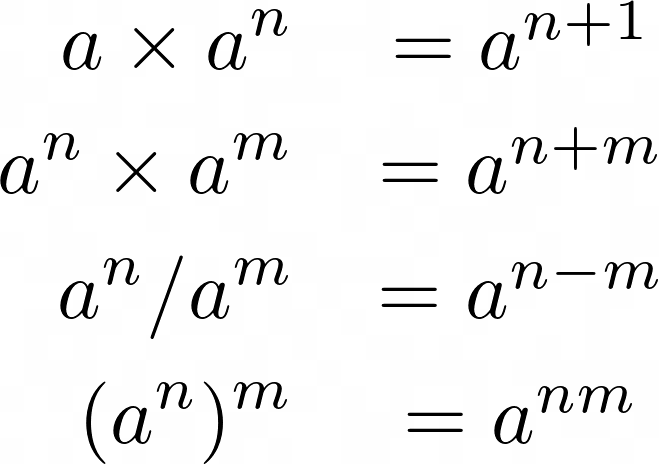
Perfect powers If b is the nth power of a for positive integers a and n, then b is called a perfect power, or a perfect nth power. In the case where b = a², b is called a perfect square.
Negative powers a⁻ⁿ is defined as 1/aⁿ.
Roots If a = bⁿ for some positive real numbers b and n, then b is the principal nth root of a. We write 
. a is called the base and n is called the root exponent. When n = 2, b is called the square root of a. When n = 3, b is called the cube root of a. The nth root of 0 is 0.
Note that exponentiation and taking roots are not inverse operations. For instance,
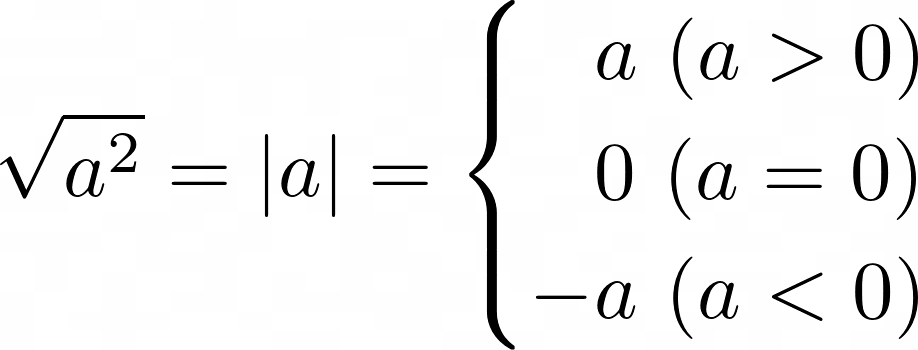
Order of operations When evaluating an expression, first perform exponentiation and roots. Then followed by multiplication and division from left to right (evaluate the numerator and denominator of any fraction first before performing the division), and finally addition and subtraction from left to right. However, any expression inside brackets should be evaluated first.
