We write a ≡ b (mod n) and say that “a is congruent to b modulo n” if n | (a – b), i.e. a – b is a multiple of n. This is also equivalent to saying that a and b have the same remainder when divided by n.
Suppose a ≡ b (mod n) and c ≡ d (mod n) for integers a, b, c, d and positive integer n. Then
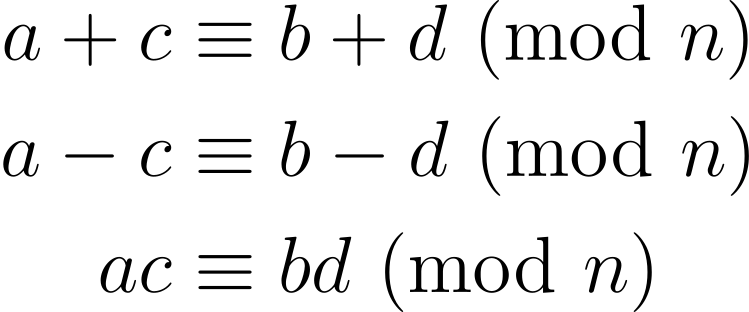
Consequently, for any positive integer k
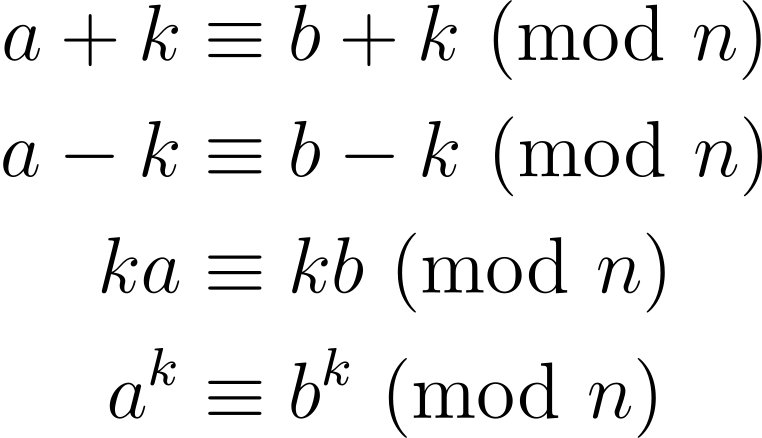
Digits
The last digit of a number is equal to the number modulo 10. This is useful when dealing with large numbers. For instance:
Qn: Find the last digit of ![]()
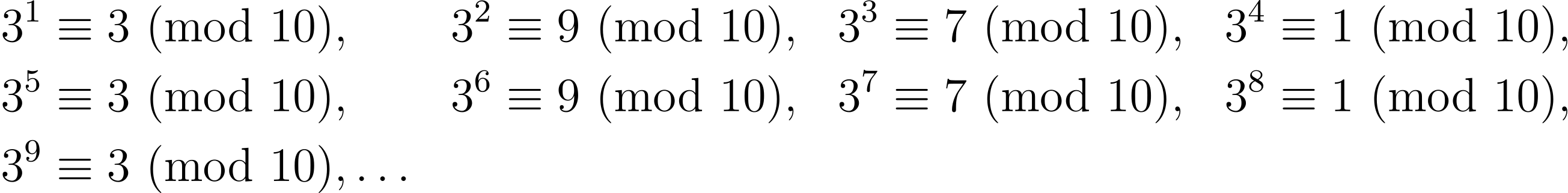
Investigating the first few powers of 3 modulo 10, we soon find a pattern. Because 3⁴ ≡ 1 (mod 10), the remainders modulo 10 repeat every fourth power. Hence
![]()
so the last digit of ![]() is 3.
is 3.
Qn: Find the last two digits of ![]()
Similarly, the last two digits of a number is its remainder when divided by 100. We have
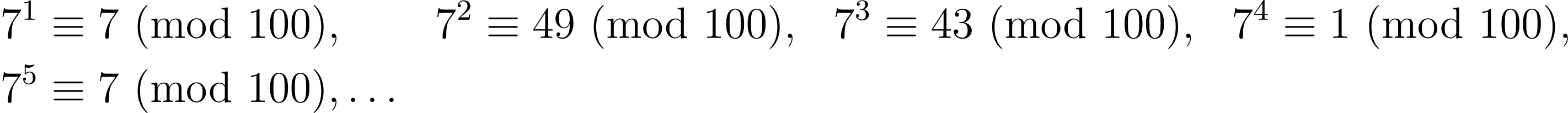
and again we see that the remainders repeat with a period of 4. So it suffices to find the remainder of the exponent 7⁷ when divided by 4. We have
![]()
Hence
![]()
and so the last two digits are 43.
Squares
Perfect squares can only have certain remainders modulo n. For instance,
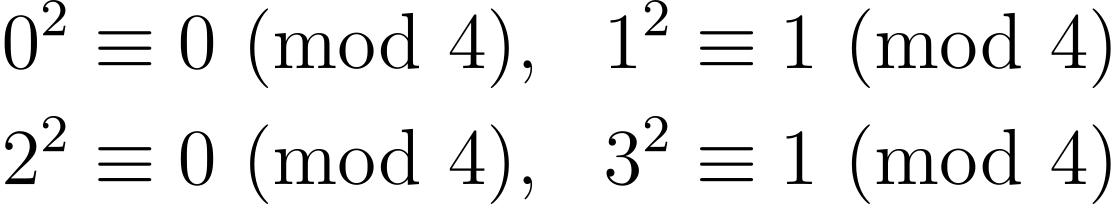
This means that the square of every even number is divisible by 4, and the square of every odd number leaves a remainder of 1 when divided by 4.
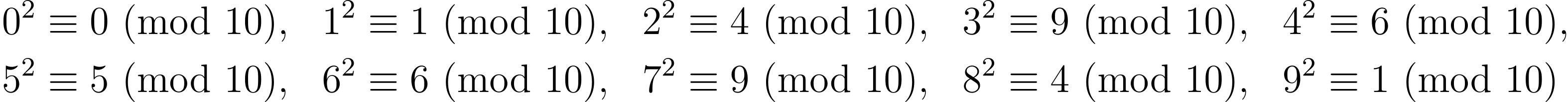
Looking at squares mod 10, we can see that the last digit of a perfect square must be either 0, 1, 4, 5 or 6.

