Natural numbers The numbers 1, 2, 3, 4, 5, … are called the natural numbers. They are also called the positive integers.
Cardinal and ordinal numbers When natural numbers represent the quantity of something, they are called cardinal numbers. For instance, if we’re talking about 3 books, ‘3’ is a cardinal number. When they represent the order that something appears in, they are called ordinal numbers. For instance, if we’re talking about the 3rd book, ‘3rd’ is an ordinal number.
Integers The integers consist of the positive integers, the negative integers and 0.
Divisibility Let a, b be integers with b ≠ 0. If there exists an integer q such that a = q · b, we say that b divides a and write b | a. If no such q exists, we say that b does not divide a and write b ∤ a.
Factors (divisors) and multiples If an integer a is divisible by an integer b (b ≠ 0), we say that a is a multiple of b and b is a factor of a. Every integer is a multiple of ±1 and ±1 is a factor of every integer. Since 0 is a multiple of every integer, every non-zero integer is a factor of 0.
Properties of the integers Let a, b, c, d, … be integers
- If a | b, then (-a) | b, a | (-b), (-a) | (-b), ∣a∣ | ∣b∣
- If a | b and b | c, then a | c
- If a | b, then a | bc
- If a | b and c ≠ 0, then ac | bc
- If ac | bc and c ≠ 0, then a | b
- If a | b and b ≠ 0, then ∣a∣ < ∣b|
- If ∣a∣ < ∣b∣ and ∣b∣ | ∣a∣, then a = 0
- If d | a and d | b, then d | (a + b) and d | (a – b)
- If
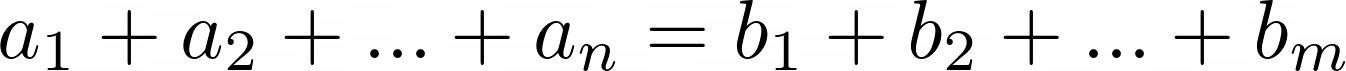, and among the (m + n) terms (m + n – 1) of them are multiples of d, then the remaining term is also a multiple of d. - Among m consecutive integers, at least one of them is divisible by m.
- (Euclid’s division lemma) For any two integers a, b with b ≠ 0, there exist unique integers q, r such that a = qb + r, with 0 ≤ r < ∣b∣. a | b precisely when r = 0
Odd numbers Integers which are not divisible by 2 are called odd numbers. Every odd number is of the form 2k + 1 for some integer k.
Even numbers Integers which are divisible by 2 are called even numbers. 0 is an even number. Every even number is of the form 2k for some integer k.
