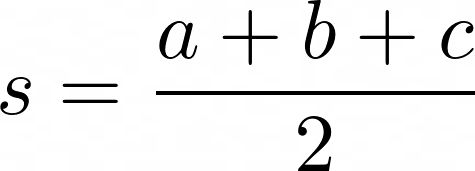Heron of Alexandria was a Greek mathematician and engineer who was active in his native city of Alexandria, Roman Egypt. He is often considered the greatest experimenter of antiquity and his work is representative of the Hellenistic scientific tradition.
Today, his name is most closely associated with Heron’s formula for finding the area of a triangle from its side lengths.
He also devised a method for calculating cube roots in the 1st century AD.
Heron’s Shortest Distance Problem
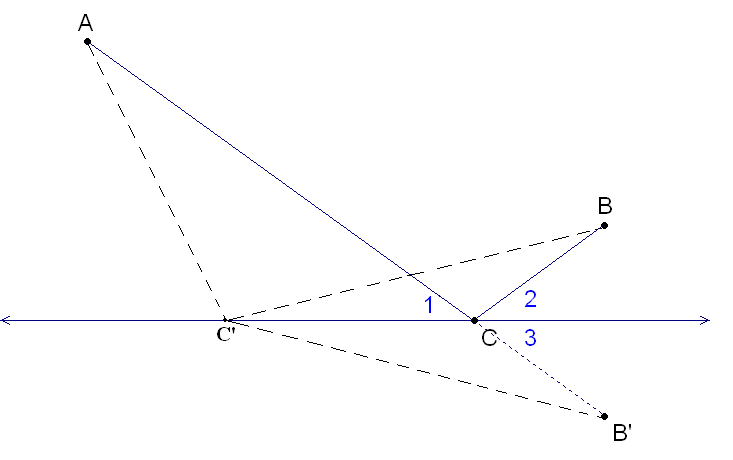
Given two points A and B on one side of a line, find a point C on the straight line, that minimizes AC + BC. The solution can be easily found by reflecting B across the line to the point B’. The length of ACB is equal to the length of ACB’, so the shortest possible path ACB corresponds to the shortest possible path ACB’, i.e. a straight line.
Heron’s Formula
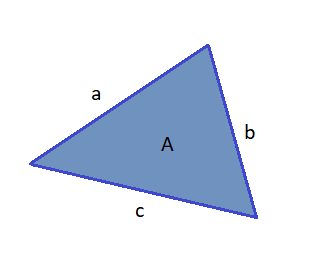
Heron’s formula gives the area of a triangle when the length of all three sides are known. Unlike other triangle area formulae, there is no need to calculate angles or other distances in the triangle first. The area of a triangle whose sides have lengths a, b, and c is:
![]()
Where s, the semiperimeter is given by: