
Leonhard Euler (15 April 1707 – 18 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who made important and influential discoveries in many branches of mathematics, such as infinitesimal calculus and graph theory, while also making pioneering contributions to several branches such as topology and analytic number theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.
Euler introduced the use of the exponential function and logarithms in analytic proofs. He discovered ways to express various logarithmic functions using power series, and he successfully defined logarithms for negative and complex numbers, thus greatly expanding the scope of mathematical applications of logarithms. He also defined the exponential function for complex numbers, and discovered its relation to the trigonometric functions.
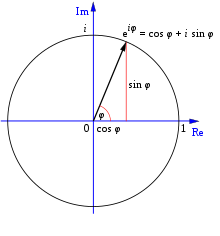
Euler’s Formula
For any real number φ (taken to be radians), Euler’s Formula states that the complex exponential function satisfies
![]()
Euler’s Identity
Setting φ = π gives the special case
![]()
This is known as Euler’s identity. Richard P. Feynman calls it “the most remarkable formula in mathematics” for single uses of the notions of addition, multiplication, exponentiation, and equality, and the single uses of the important constants 0, 1, e, i and π. In 1988, readers of the Mathematical Intelligencer voted it “the Most Beautiful Mathematical Formula Ever”. In total, Euler was responsible for three of the top five formulae in that poll.

