A quadratic polynomial is an expression of the form ax² + bx + c, where a, b, c are constants (a ≠ 0) and x is a variable. A root of the quadratic polynomial is a value for x such that ax² + bx + c = 0. Rearranging, we get
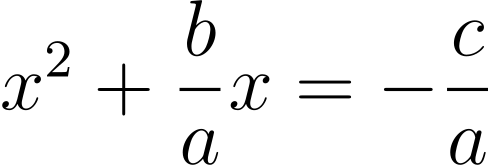
An expression like y² + py = q is difficult to solve, but something like y² = q is easy. We can transform the LHS into an easier expression using a clever trick called completing the square:
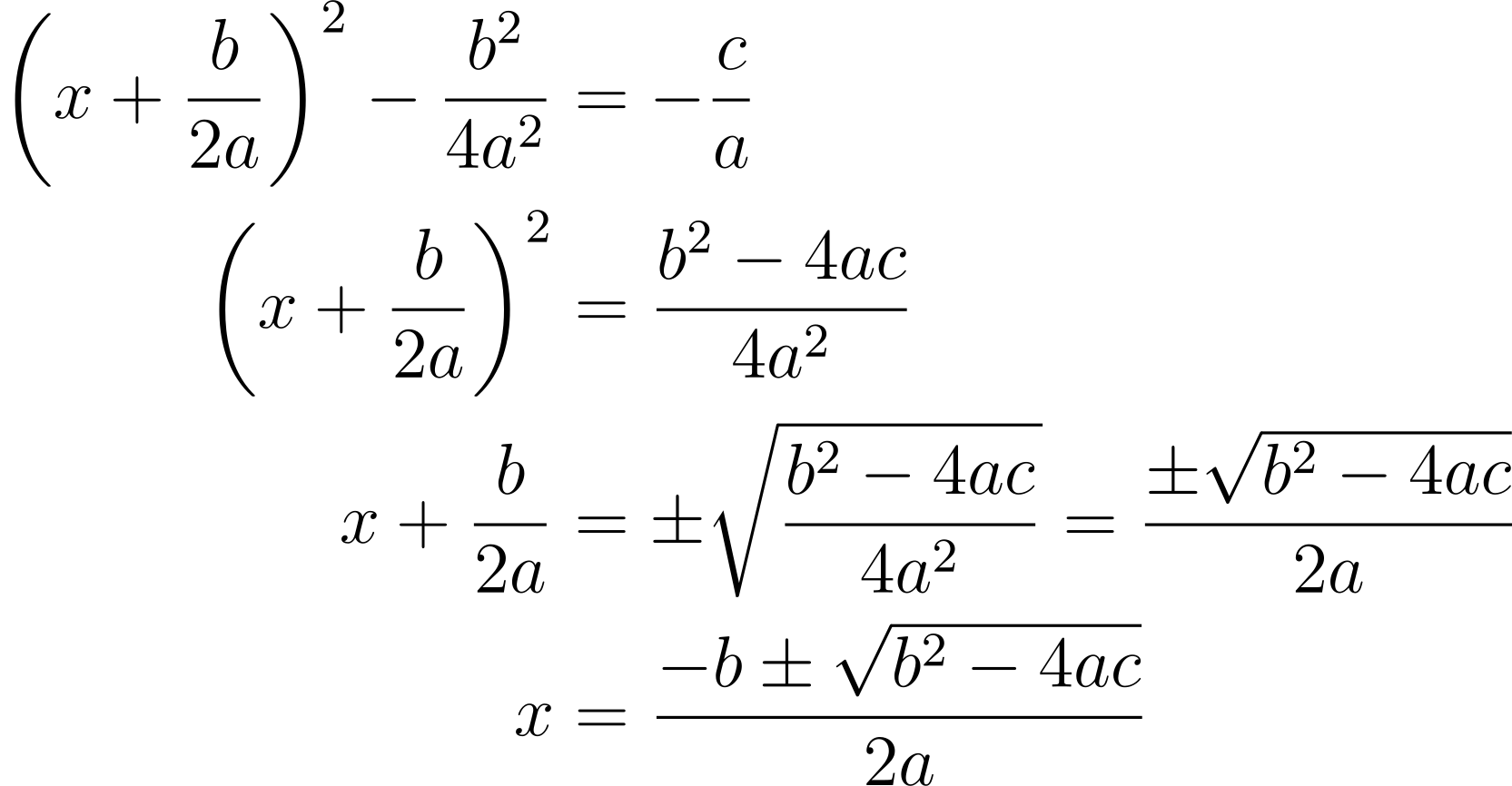
This trick can be used to solve problems where quadratic-like expressions appear.
(AIME 2008) There exist unique positive integers x and y that satisfy the equation x²+84x+2008 = y². Find x + y.
Solution: We can express the LHS as (x + 42)² + 244. Hence 244 = y² – (x + 42)² = (y + x + 42)(y – x – 42), and so y + x + 42 and y – x – 42 must both be factors of 244 of the same parity. The prime factorization of 244 is 2² ∙ 61, and the only way to express it as a product of two numbers of the same parity is 244 = 2 ∙ 122. Hence y + x + 42 = 122 and x + y = 80.
(SSSMO Junior 2006) Suppose α, β are the two roots of the equation
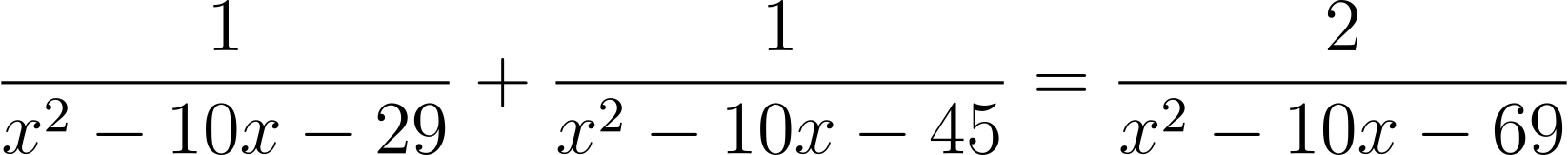
Find α + β.
Solution: Notice that all the terms have x² – 10 in the denominator. This suggests we try the substitution y = (x – 5)². The equation becomes
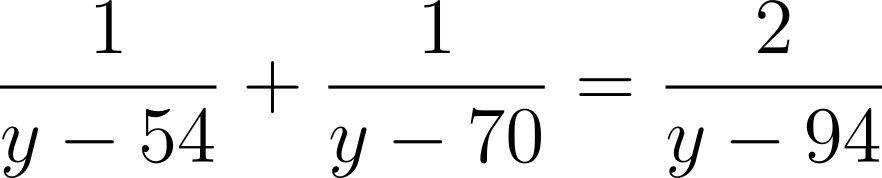
Clearing denominators gives
![]()
Expanding:
![]()
Solving for y, we get y = 64. Hence (x – 5)² = 64, so the two roots are 13 and -3 and their sum is 10.
(SMO 2013) Let x and y be real numbers satisfying
![]()
Find x² + y².
Solution: There are two squares to complete:
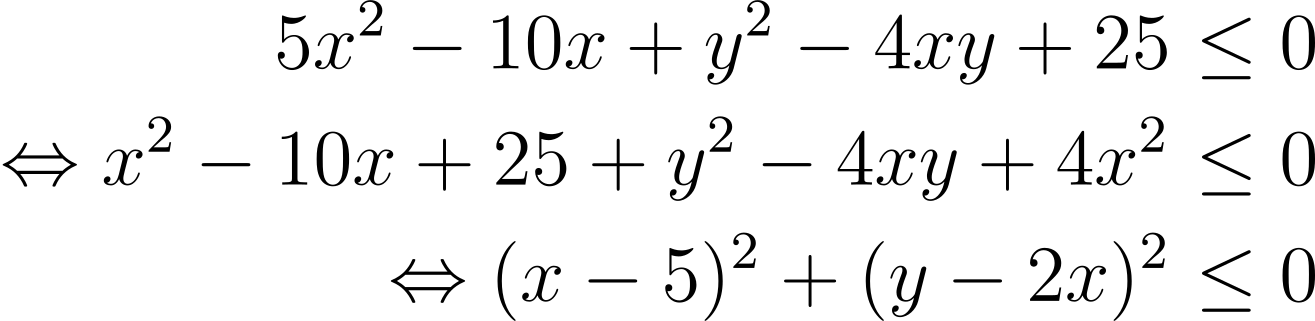
This can only occur when x – 5 and y – 2x are both 0, i.e x = 5, y = 10, and so x² + y² = 125.

